Hukum Ohm untuk rantai lengkap dan untuk bahagian rantai: pilihan untuk menulis formula, penerangan dan penjelasan

Tiada cara untuk juruelektrik profesional atau pakar elektronik untuk memintas undang-undang Ohm dalam aktivitinya sendiri, menyelesaikan sebarang masalah yang berkaitan dengan persediaan, pelarasan dan pembaikan litar elektronik dan elektrik.

Sebenarnya, semua orang perlu memahami undang-undang ini. Kerana setiap orang terpaksa berhadapan dengan elektrik dalam kehidupan seharian.

Dan walaupun undang-undang ahli fizik Jerman Ohm diperuntukkan dalam kurikulum sekolah menengah, dalam praktiknya ia tidak selalu dipelajari tepat pada masanya. Oleh itu, dalam bahan kami, kami akan mempertimbangkan topik yang relevan untuk kehidupan dan memahami pilihan untuk menulis formula.

Bahagian tunggal dan litar elektrik lengkap

Memandangkan litar elektrik dari sudut pandangan menggunakan hukum Ohm pada litar, dua pilihan pengiraan yang mungkin perlu diperhatikan: untuk bahagian berasingan dan untuk litar penuh.

Pengiraan arus bahagian litar elektrik

Bahagian litar elektrik, sebagai peraturan, dianggap sebagai bahagian litar yang mengecualikan sumber EMF, sebagai mempunyai rintangan dalaman tambahan.

Oleh itu, formula pengiraan, dalam kes ini, kelihatan mudah:

I = U/R,

Di mana, masing-masing:

• saya – kekuatan semasa;
• U – voltan yang digunakan;
• R - rintangan.

Tafsiran formula adalah mudah - arus yang mengalir melalui bahagian tertentu litar adalah berkadar dengan voltan yang digunakan padanya, dan rintangan adalah berkadar songsang.

Grafik yang dipanggil "daisy", di mana keseluruhan set variasi rumusan berdasarkan hukum Ohm dibentangkan. Alat mudah untuk penyimpanan poket: sektor "P" - formula kuasa; sektor "U" - formula voltan; sektor "I" - formula semasa; sektor "R" - formula rintangan

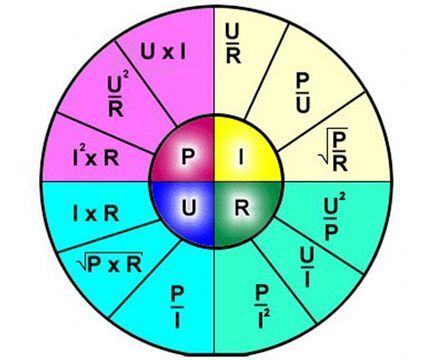
Oleh itu, formula dengan jelas menerangkan pergantungan aliran semasa melalui bahagian berasingan litar elektrik berbanding dengan nilai voltan dan rintangan tertentu.

Formula ini mudah digunakan, sebagai contoh, apabila mengira parameter rintangan yang perlu dipateri ke dalam litar jika voltan dan arus diberikan.

Undang-undang Ohm dan dua akibat yang mesti diketahui oleh setiap jurutera elektromekanikal profesional, jurutera elektrik, jurutera elektronik dan sesiapa sahaja yang terlibat dalam pengendalian litar elektrik. Dari kiri ke kanan: 1 - penentuan semasa; 2 - penentuan rintangan; 3 - definisi voltan, di mana I - semasa, U - voltan, R - rintangan

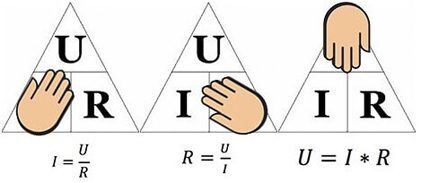
Angka di atas akan membantu menentukan, sebagai contoh, arus yang mengalir melalui rintangan 10-ohm yang mana voltan 12 volt digunakan. Menggantikan nilai, kita dapati – I = 12 / 10 = 1.2 ampere.

Masalah mencari rintangan (apabila arus dan voltan diketahui) atau voltan (apabila voltan dan arus diketahui) diselesaikan dengan cara yang sama.

Oleh itu, anda sentiasa boleh memilih voltan operasi yang diperlukan, kekuatan arus yang diperlukan dan elemen rintangan yang optimum.

Formula yang dicadangkan untuk digunakan tidak memerlukan mengambil kira parameter sumber voltan.Walau bagaimanapun, litar yang mengandungi, sebagai contoh, bateri, akan dikira menggunakan formula yang berbeza. Dalam rajah: A – menghidupkan ammeter; V – hidupkan voltmeter.

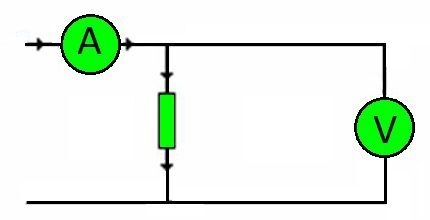
Dengan cara ini, wayar penyambung mana-mana litar adalah rintangan. Jumlah beban yang perlu mereka tanggung ditentukan oleh voltan.

Oleh itu, sekali lagi menggunakan undang-undang Ohm, adalah mungkin untuk memilih keratan rentas konduktor yang diperlukan dengan tepat, bergantung pada bahan teras.

Kami mempunyai arahan terperinci di laman web kami pengiraan keratan rentas kabel dari segi kuasa dan arus.

Pilihan pengiraan untuk rantaian lengkap

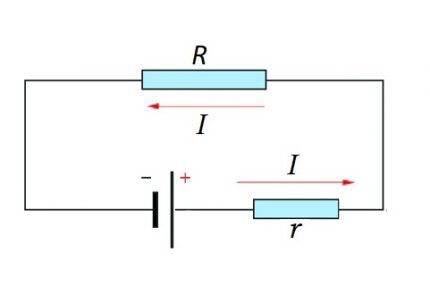
Litar lengkap terdiri daripada bahagian (bahagian), serta sumber EMF. Iaitu, sebenarnya, rintangan dalaman sumber EMF ditambah kepada komponen rintangan sedia ada bahagian litar.

Oleh itu, adalah logik untuk mengubah sedikit formula di atas:

I = U / (R + r)

Sudah tentu, nilai rintangan dalaman EMF dalam undang-undang Ohm untuk litar elektrik yang lengkap boleh dianggap boleh diabaikan, walaupun nilai rintangan ini sebahagian besarnya bergantung pada struktur sumber EMF.

Walau bagaimanapun, apabila mengira litar elektronik kompleks, litar elektrik dengan banyak konduktor, kehadiran rintangan tambahan adalah faktor penting.

Untuk pengiraan di bawah keadaan litar elektrik yang lengkap, nilai rintangan sumber EMF sentiasa diambil kira. Nilai ini dijumlahkan dengan rintangan rintangan litar elektrik itu sendiri. Dalam rajah: I - aliran semasa; R—elemen rintangan luaran; r ialah faktor rintangan EMF (sumber tenaga)

Kedua-dua untuk bahagian litar dan untuk litar lengkap, momen semula jadi harus diambil kira - penggunaan arus malar atau berubah-ubah.

Jika perkara-perkara yang dinyatakan di atas, ciri-ciri undang-undang Ohm, dipertimbangkan dari sudut pandangan menggunakan arus terus, oleh itu dengan arus ulang-alik semuanya kelihatan agak berbeza.

Pertimbangan kesan undang-undang ke atas kuantiti berubah

Konsep "rintangan" kepada syarat-syarat yang mengalirkan arus ulang-alik harus dianggap lebih seperti konsep "impedans". Ini merujuk kepada gabungan beban perintang (Ra) dan beban perintang reaktif (Rr).

Fenomena sedemikian disebabkan oleh parameter unsur induktif dan undang-undang pensuisan berhubung dengan nilai voltan berubah - nilai arus sinusoidal.

Ini ialah litar setara bagi litar elektrik arus ulang alik untuk pengiraan menggunakan rumusan berdasarkan prinsip hukum Ohm: R - komponen perintang; C ialah komponen kapasitif; L—komponen induktif; EMF ialah sumber tenaga; I - aliran semasa

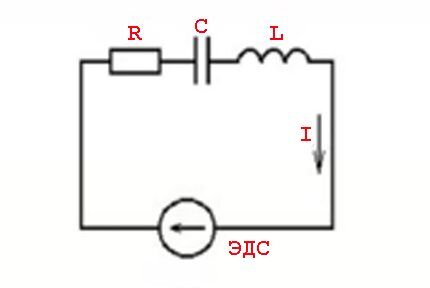
Dalam erti kata lain, terdapat kesan nilai semasa mendahului (lag) daripada nilai voltan, yang disertai dengan penampilan kuasa aktif (resistif) dan reaktif (induktif atau kapasitif).

Fenomena sedemikian dikira menggunakan formula:

Z=U/I atau Z = R + J * (X_L -X_C)

di mana: Z – impedans; R - beban aktif; X_L , X_C – beban induktif dan kapasitif; J - pekali.

Sambungan bersiri dan selari bagi elemen

Untuk elemen litar elektrik (bahagian litar), titik ciri ialah sambungan bersiri atau selari.

Sehubungan itu, setiap jenis sambungan disertakan dengan corak aliran arus dan bekalan voltan yang berbeza.Dalam hal ini, hukum Ohm juga digunakan secara berbeza, bergantung pada pilihan untuk memasukkan unsur.

Litar elemen perintang bersambung siri

Berhubung dengan sambungan siri (bahagian litar dengan dua komponen), rumusan berikut digunakan:

• saya = saya₁ = saya₂ ;
• U = U₁ +U₂ ;
• R = R₁ + R₂

Rumusan ini jelas menunjukkan bahawa, tanpa mengira bilangan komponen rintangan yang disambungkan secara bersiri, arus yang mengalir melalui bahagian litar tidak berubah dalam nilai.

Sambungan elemen perintang dalam bahagian litar secara bersiri antara satu sama lain. Pilihan ini mempunyai undang-undang pengiraan sendiri. Dalam rajah: I, I1, I2 - aliran semasa; R1, R2 - unsur rintangan; U, U1, U2 - voltan terpakai

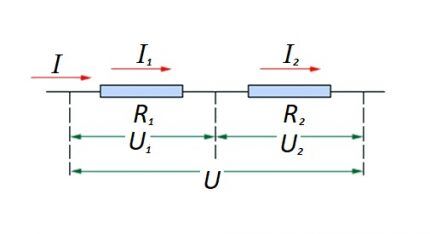
Magnitud voltan yang digunakan pada komponen rintangan berkesan litar ialah jumlah dan jumlah nilai sumber emf.

Dalam kes ini, voltan pada setiap komponen individu adalah sama dengan: Ux = I * Rx.

Jumlah rintangan harus dianggap sebagai jumlah nilai semua komponen rintangan dalam litar.

Litar unsur perintang bersambung selari

Dalam kes apabila terdapat sambungan selari komponen rintangan, rumusan berikut dianggap adil berhubung dengan undang-undang ahli fizik Jerman Ohm:

• saya = saya₁ +Saya₂ … ;
• U = U₁ =U₂ … ;
• 1/R = 1/R₁ + 1/R₂ + …

Pilihan untuk membuat bahagian litar jenis "bercampur", apabila sambungan selari dan bersiri digunakan, tidak dikecualikan.

Sambungan elemen perintang pada bahagian litar selari antara satu sama lain. Untuk pilihan ini, undang-undang pengiraan yang berbeza digunakan. Dalam rajah: I, I1, I2 - aliran semasa; R1, R2 - unsur rintangan; U ialah voltan yang dibekalkan; A, B - titik masuk/keluar

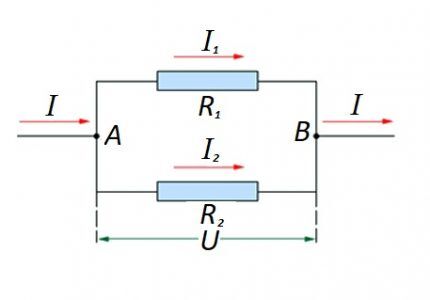
Untuk pilihan sedemikian, pengiraan biasanya dilakukan dengan mengira peringkat perintang sambungan selari pada mulanya. Kemudian nilai perintang yang disambungkan secara bersiri ditambah kepada hasil yang diperoleh.

Bentuk undang-undang integral dan pembezaan

Semua titik di atas dengan pengiraan adalah terpakai kepada keadaan apabila konduktor, boleh dikatakan, struktur "homogen" digunakan dalam litar elektrik.

Sementara itu, dalam amalan, seseorang sering perlu berurusan dengan pembinaan skema, di mana struktur konduktor berubah dalam bahagian yang berbeza. Sebagai contoh, wayar keratan rentas yang lebih besar atau, sebaliknya, yang lebih kecil, diperbuat daripada bahan yang berbeza, digunakan.

Untuk mengambil kira perbezaan tersebut, terdapat variasi yang dipanggil "hukum Ohm kamiran pembezaan." Untuk konduktor yang sangat kecil, tahap ketumpatan semasa dikira bergantung kepada voltan dan nilai kekonduksian.

Formula berikut digunakan untuk pengiraan pembezaan: J = ό * E

Untuk pengiraan kamiran, rumusan adalah: I * R = φ1 – φ2 + έ

Walau bagaimanapun, contoh-contoh ini agak lebih dekat dengan sekolah matematik yang lebih tinggi dan sebenarnya tidak digunakan dalam amalan sebenar juruelektrik mudah.

Kesimpulan dan video berguna mengenai topik ini

Analisis terperinci tentang undang-undang Ohm dalam video di bawah akan membantu akhirnya menyatukan pengetahuan ke arah ini.

Pelajaran video unik secara kualitatif mengukuhkan pembentangan bertulis teori:

Kerja juruelektrik atau aktiviti jurutera elektronik berkait rapat dengan saat-saat apabila seseorang itu benar-benar perlu mematuhi undang-undang Georg Ohm dalam tindakan. Ini adalah beberapa jenis truism yang perlu diketahui oleh setiap profesional.

Pengetahuan yang luas mengenai isu ini tidak diperlukan - cukup untuk mempelajari tiga variasi utama perkataan untuk berjaya menerapkannya dalam amalan.

Adakah anda ingin menambah bahan di atas dengan komen yang berharga atau menyatakan pendapat anda? Sila tulis komen di blok di bawah artikel. Jika anda mempunyai sebarang soalan, jangan teragak-agak untuk bertanya kepada pakar kami.